Question

The numerical value of sin²5° + sin²10° + sin²15° +... sin²85° + sin²90° is equal a) 17/2 b) 19/2 c) 15/2 d) 13/2​

Answer 1

Answer:
`b)~\Large\boxed{(19)/(2) }`

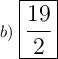
Explanation:

Given expression

sin²5° + sin²10° + sin²15° +... sin²85° + sin²90°

Concept:

sin²x + cos²x = 1

sin(x) = cos (90 - x)

There are in total these terms:

5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90

In total, there are 18 terms, and the first one matches with the second to the last one:

5 -- 85

10 -- 80

.

.

.

40 -- 50

There are 2 terms left over:

sin²45 and sin²90

Convert the first half of the sine terms (sin²5 - sin²40) to the cosine terms

sin²5 = cos² (90 - 5) = cos²85

sin²10 = cos² (90 - 10) = cos²80

.

.

.

sin²40 = cos² (90 - 40) = cos²50

Simplify the 16 grouped terms

i.e. sin²85 and cos²85

Using the concept of sin²x + cos²x = 1

sin²85 + cos²85 = 1

sin²80 + cos²80 = 1

.

.

.

sin²50 + cos²50 = 1

Total = (16/2) × 1 = 8 × 1 = 8

Evaluate the 2 terms that are left over

sin²45 = (sin45) (sin45) = (√2 / 2) (√2 / 2) = 1/2

sin²90 = (sin90) (sin 90) = (1) (1) = 1

Add all the terms together

`8+(1)/(2) +1=\Large\boxed{(19)/(2) }`

Hope this helps!! :)

Please let me know if you have any questions