Question

Which graph represents the equation

Answer 1

First graph

Explanation:

To identify which graph represents the equation, we can find an x-intercept of a function by substituting y = 0 in.

That will result with
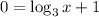`\displaystyle{0 = \log_3 x + 1}`. Then we solve the equation for x:

`\displaystyle{-1 = \log_3 x}`

Apply logarithm conversion to exponential:

`\displaystyle{\log_a b = n \to a^n = b}`

Therefore:

`\displaystyle{\log_3 x = -1 \to 3^(-1) = x}`

Apply law of exponent for negative exponent to simplify:

`\displaystyle{a^(-n) = (1)/(a^n)}`

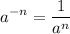
Therefore:

`\displaystyle{x = 3^(-1)}\\\\\displaystyle{x = (1)/(3)}`

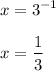
Since the logarithm has positive integer base then we can cut off choice 2 and choice 3 since that only applies to negative logarithm and fraction base of logarithm.

The only choices we have are first and fourth but fourth graph has x-intercept equal to 3. However, we solve for x-intercept and receive 1/3 as our x-intercept which is between 0 and 1.

Henceforth, the first graph represents the equation.