Answer:
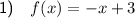
2) A = (3, 0) and C = (-3, 0)
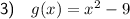
4) AC = 6 units and OB = 9 units
Explanation:
Given functions:
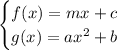
Part (1)
Given points:
As points H and T lie on f(x), substitute the two points into the function to create two equations:
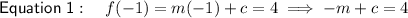
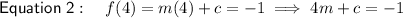
Subtract the first equation from the second to eliminate c:
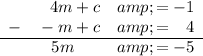
Therefore m = -1.
Substitute the found value of m and one of the points into the function and solve for c:
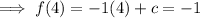
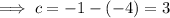
Therefore the equation for function f(x) is:
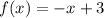
Part (2)
Function f(x) crosses the x-axis at point A. Therefore, f(x) = 0 at point A.
To find the x-value of point A, set f(x) to zero and solve for x:
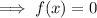
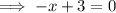
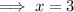
Therefore, A = (3, 0).
As g(x) = ax² + b, its axis of symmetry is x = 0.
A parabola's axis of symmetry is the midpoint of its x-intercepts.
Therefore, if A = (3, 0) then C = (-3, 0).
Part (3)
Points on function g(x):
Substitute the points into the given function g(x) to create two equations:
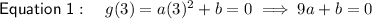
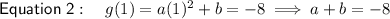
Subtract the second equation from the first to eliminate b:
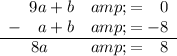
Therefore a = 1.
Substitute the found value of a and one of the points into the function and solve for b:
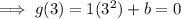
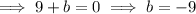
Therefore the equation for function g(x) is:
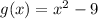
Part 4
The length AC is the difference between the x-values of points A and C.
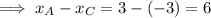
Point B is the y-intercept of g(x), so when x = 0:
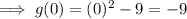
Therefore, B = (0, -9).
The length OB is the difference between the y-values of the origin and point B.
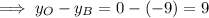
Therefore, AC = 6 units and OB = 9 units