Hi, there!
To solve the function operation, let's start by writing 25 everywhere we see x:

________
Now here's the most important part - The order of operations.
It's vital in simplifying expressions with multiple operations, like this one.
There's an acronym that will help you remember the order of operations.
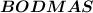
Here,
- B = Brackets. The first of all these operations, the Brackets operation tells us to simplify all expressions with brackets, if we have any.
- O = order of exponents. This operation comes right after brackets. Once we've evaluated all the expressions with the brackets, we can start evaluating exponential expressions.
- D = division & M = multiplication. Unlike the two operations above, these two operations are interchangeable; you can do division first, and then multiplication, or the other way around.
- A = addition & S=Subtraction. Just like the two operations above, these two guys are also interchangeable.
_________
Now let's get down to evaluating our expression.
We have
- Exponents
- Multiplication
- Addition
- Subtraction

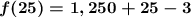
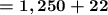
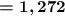
Hope the answer - and explanation - made sense,
happy studying!!