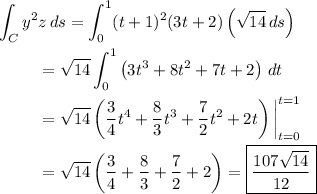I assume each path
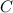 is oriented positively/counterclockwise.
is oriented positively/counterclockwise.
(a) Parameterize
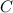 by
by

with
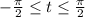 . Then the line element is
. Then the line element is
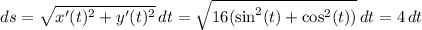
and the integral reduces to
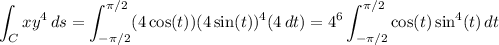
The integrand is symmetric about
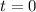 , so
, so
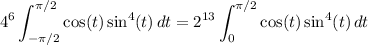
Substitute
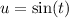 and
and
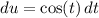 . Then we get
. Then we get
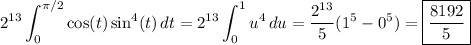
(b) Parameterize
 by
by
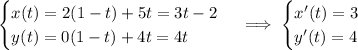
with
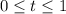 . Then
. Then
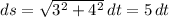
and
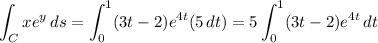
Integrate by parts with
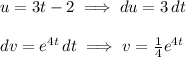
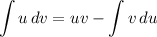
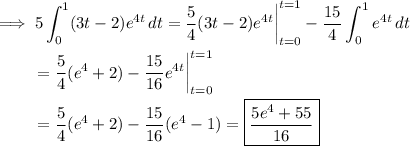
(c) Parameterize
 by
by
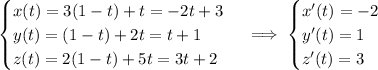
with
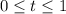 . Then
. Then
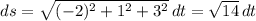
and