Answer:
sin(θ₁) = (√357)/29
Explanation:
The relationship between sine and cosine can be used to find sin(θ₁).
Sine
In Quadrant II, the sine is positive. The sine is given in terms of the cosine by ...
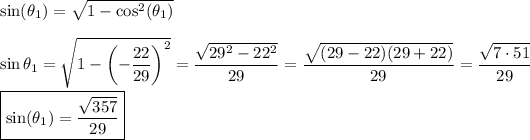
__
Additional comment
We didn't have to use the factoring of the difference of squares to evaluate the radical. However, by doing so, we could see that the value had no square factors that would permit it to be simplified.