Question

Graph the line that passes through the points (6,-4) and (3,-6) and determine

the equation of the line.

Answer 1

`y = \frac23x - 8`

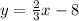
Explanation:

Hello!

First, let's plot the points and draw a straight line through them (image).

Remember that a coordinate is given in the format of (x,y).

Parts of a Line

Equation format:
`y = mx + b`

• m = slope
• b = y-intercept

The slope is how the graph changes in y as it does in x. Given our two points, the graph rises 2 units and runs 3. That means that the slope is
`\frac23`.

• 
  `y = \frac23x + b`

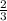The y-intercept is the intersection of the graph and the y-axis. The intersection takes place at y = -8, so the y-intercept is -8.

• 
  `y = \frac23x - 8`

The equation is
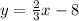`y = \frac23x - 8`.