Question

Let
`f(x,y) = (x^(2) y)/(x^(4)+y^(2) )` .

Which of the following is true about
`\lim_((x,y) \to \((0,0)) f(x,y)` ?

Answer 1

The correct answer is C.

The limit in A does exist:

`\displaystyle \lim_(x\to0) f(x,0) = \lim_(x\to0) \frac0{x^4} = 0`

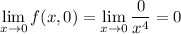
The limit in B also exists: for any
`k\in\Bbb R`,

`\displaystyle \lim_(x\to0) f(x,kx) = \lim_(x\to0) (kx^3)/(x^4+k^2x^2) = \lim_(x\to0)(kx)/(x^2+k^2) = 0`

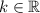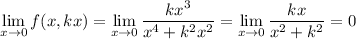
But this alone does not prove the 2D limit exists.
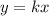`y=kx` only captures all the paths through the origin that are straight lines.

The limit in C also exists, but it's not the same as either of the limits along the paths used in A and B.

`\displaystyle \lim_(x\to0) f(x,x^2) = \lim_(x\to0) (x^4)/(2x^4) = \frac12`

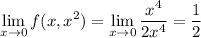
That this value is non-zero tells us the original limit does not exist.

The claim in D is generally not correct. That
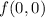`f(0,0)` is undefined does not automatically mean the limit doesn't exist. A simpler example:

`\displaystyle \lim_(x\to0) (x)/(x) = \lim_(x\to0) 1 = 1`

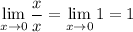
yet
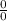`\frac00` is undefined.