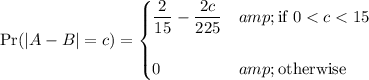Question

Given a, b such that both a and b are real numbers between 0 and 15, what is the probability for |a-b|

Answer 1

I guess you're asking about the probability density for the random variable
`|A-B|` where
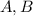`A,B` are independent and identically distributed uniformly on the interval (0, 15). The PDF of e.g.
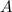`A` is

`\mathrm{Pr}(A=a) = \begin{cases}\frac1{15} & \text{if } 0 < a < 15 \\\\ 0 & \text{otherwise}\end{cases}`

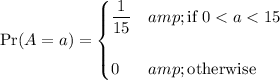
It's easy to see that the support of
`|A-B|` is the same interval, (0, 15), since
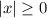`|x|\ge0`, and

• at most, if
`A=15` and
`B=0`, or vice versa, then
`|A-B|=15`

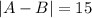
• at least, if
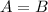`A=B`, then
`|A-B|=0`

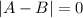
Compute the CDF of
`C=|A-B|` :

`\mathrm{Pr}(C\le c) = \mathrm{Pr}(|A - B| \le c) = \mathrm{Pr}(-c \le A - B \le c)`

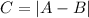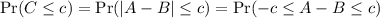
This probability corresponds to the integral of the joint density of
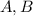`A,B` over a subset of a square with side length 15 (see attached). Since
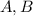`A,B` are independent, their joint density is

`\mathrm{Pr}(A=a,B=b) = \begin{cases}\frac1{15^2} & \text{if } (a,b) \in (0,15) * (0,15) \\ 0 &\text{otherwise}\end{cases}`

The easiest way to compute this probability is by using the complementary region. The triangular corners are much easier to parameterize.

`\displaystyle \mathrm{Pr}(|A-B|\le c) = 1 - \mathrm{Pr}(|A-B| > c) \\\\ ~~~~~~~~ = 1 - \int_0^(15-c) \int_(a+c)^(15) (db\,da)/(15^2) - \int_c^(15) \int_0^(a-c) (db\,da)/(15^2) \\\\ ~~~~~~~~ = 1 - \frac1{225} \left(\int_0^(15-c) (15 - a - c) \, da + \int_c^(15) (a - c) \, da\right)`

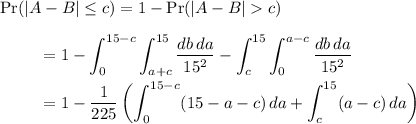
In the second integral, substitute
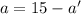`a=15-a'` and
`da=-da'`, so that

`\displaystyle \int_c^(15) (a-c) \, da = \int_(15-c)^0 (15-a'-c) (-da') = \int_0^(15-c) (15 - a' - c) \, da'`

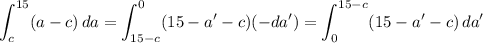
which is the same as the first integral. This tells us the joint density is symmetric over the two triangular regions.

Then the CDF is

`\displaystyle \mathrm{Pr}(|A-B|\le c) = 1 - \frac2{225} \int_0^(15-c) (15 - a - c) \, da \\\\ ~~~~~~~~ = 1 - \frac2{225} \left((15-c) a - \frac12 a^2\right) \bigg|_(a=0)^(a=15-c) \\\\ ~~~~~~~~ = \begin{cases}0 & \text{if } c < 0 \\\\ 1 - ((15-c)^2)/(225) = (2c)/(15) - (c^2)/(225) & \text{if } 0 \le c < 15 \\\\ 1 & \text{if } c \ge 15\end{cases}`

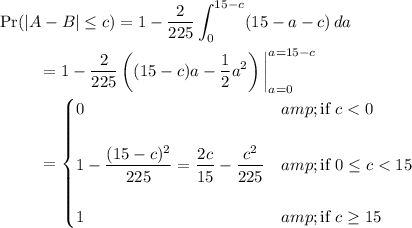
We recover the PDF by differentiating with respect to
`c`.

`\mathrm{Pr}(|A-B| = c) = \begin{cases}\frac2{15} - (2c)/(225) & \text{if } 0 < c < 15 \\\\ 0 & \text{otherwise}\end{cases}`