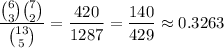The number of combinations of size
 that you can make with
that you can make with
 items is given by the so-called binomial coefficient,
items is given by the so-called binomial coefficient,
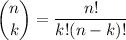
•
 is the number of ways of permuting
is the number of ways of permuting
 items.
items.
•
 is the number of ways of permuting all but
is the number of ways of permuting all but
 of the
of the
 items.
items.
Dividing
 by
by
 then gives the number of ways of permuting only
then gives the number of ways of permuting only
 of the total
of the total
 items.
items.
•
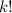 is the number of ways of permuting
is the number of ways of permuting
 items.
items.
Dividing
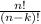 by
by
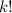 then removes all those permutations which contain the same items. We call these combinations.
then removes all those permutations which contain the same items. We call these combinations.
For this problem we only care about counting combinations.
There are
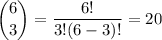
ways of selecting any 3 girls from the total 6 girls in the entire group of people.
There are
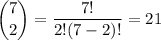
was of selecting any 2 boys from the total 7 boys.
Then there are
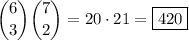
ways of choosing a committee of 5 people consisting of 3 girls and 2 boys.
If the next question were, "What is the probability that a committee of 5 randomly selected people consists of 3 girls and 2 boys?", then you would additionally need to compute the number of ways one can make a committee of 5 people from the total 13, which is
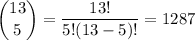
Then the probability of selecting such a committee at random is