Question

what is the general form of the solutions of a linear homogeneous recurrence relation if its characteristic equatino has roots 1,1,1,1,-2,-2,-2,3,3,-4

Answer 1

If the root 1 has multiplicity 4, -2 has multiplicity 3, 3 has multiplicity 3, and -4 is a single root, then the homogeneous solution has the form

`\left(C_(1,0)+C_(1,1)n+C_(1,2)n^2+C_(1,3)n^3\right) 1^n \\\\ ~~~~~~~~ + \left(C_(-2,0)+C_(-2,1)n+C_(-2,2)n^2\right) (-2)^n \\\\ ~~~~~~~~ + \left(C_(3,0)+C_(3,1)n\right) 3^n + C_(-4,0) (-4)^n`

where
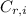`C_(r,i)` just means the arbitrary constant attached to the
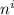`n^i` term corresponding to the root
`r` of the characteristic polynomial.