Question

The functions $f$ and $g$ are defined as follows: \[f(x) = \sqrt{\dfrac{x+1}{x-1}}\quad\text{and}\quad g(x) = \dfrac{\sqrt{x+1}}{\sqrt{x-1}}. \]explain why the functions $f$ and $g$ are not the same function.

Answer 1

Recall that √x has a domain of x ≥ 0.

So, f(x) is defined as long as

(x + 1)/(x - 1) ≥ 0

• We have equality when x = -1

• Otherwise (x + 1)/(x - 1) is positive if both x + 1 and x - 1 are positive, or both are negative:

`\begin{cases}x+1>0 \implies x>-1 \\ x-1>0 \implies x>1\end{cases} \implies x > 1`

`\begin{cases}x+1<0 \implies x<-1 \\ x-1<0 \implies x<1\end{cases} \implies x<-1`

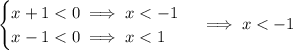
Then the domain of f(x) is

x > 1 or x ≤ -1

On the other hand, g(x) is defined by two individual square root expressions with respective domains of

• x + 1 ≥ 0 ⇒ x ≥ -1

• x - 1 ≥ 0 ⇒ x ≥ 1

but note that g(1) is undefined, so we omit it from the second domain.

Then g(x) is defined so long as both x ≥ -1 *and* x > 1 are satisfied, which means its domain is

x > 1

f(x) and g(x) have different domains, so they are not the same function.