Question

The longest amount of time employees can work under Option A or Option B is 20 weeks. After employees

work 20 weeks, they can either quit or keep making the same amount they made during Week 20. If an

employee plans on quitting after 20 weeks, which payment option gives the greatest total income? Explain.

after the 6th week on the table, the pattern continues


The table and payment per week is below!

Answer 1

Option A

Explanation:

Option A is an arithmetic sequence.

Each week, the salary goes up by a fixed $50.

To verify this, subtract any two consecutive weeks' salaries.

For example: $250 - $200 = $50; $350 - $300 = $50, etc.

The common difference in 50.

We have an arithmetic sequence with 20 terms. The first term is $200. We need to find the sum of the 20 terms.

The sum of an arithmetic sequence is given by the formula:

`S_n = (n)/(2) * [2a_1 + (n - 1)d]`

S_n = sum of first n terms

n = number of terms = 20

a_1 = first term = 200

d = common difference = 50

`S_(20) = (20)/(2) * [2(200) + (20 - 1)(50)]`

`S_(20) = 10 * [400 + 19(50)]`

`S_(20) = 10 * [400 + 19(50)]`

`S_(20) = 13500`

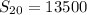
Option A gives a total of $13,500 for the first 20 weeks.

Option B is a geometric sequence in which the salary goes up by 10% each week. To verify this, divide any salary by the previous week's salary.

For example: $220/$200 = 1.10; $266.20/$242 = 1.10; in each case, each salary is 1.1 times the previous week's salary which means a 10% increase. The common ratio of the geometric sequence is 1.1.

We need the formula for the sum of the first n terms of a geometric sequence.

`S_n = (a_1(1 - r^n))/(1 - r)`

`S_(20) = (200(1 - 1.1^(20)))/(1 - 1.1)`

`S_(20) = (200(1 - 6.7274999))/(-0.1)`

`S_(20) = 11455`

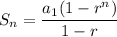
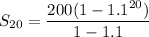
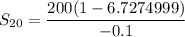
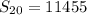
Option B gives a total of $11,455 for the first 20 weeks.

Answer: Option A