Answer:
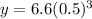
Explanation:
half-life of 14 days, basically means it reduces by 50% or half every 14 days.
This can generally be expressed as:
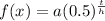 , where h=half life, and t=time, where the unit of time for t and half-life is the same. also a is the initial value.
, where h=half life, and t=time, where the unit of time for t and half-life is the same. also a is the initial value.
So we can express this half-life equation as:
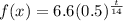 where t=days.
where t=days.
So plugging in 42 days in here, we get:

The reason for this is because 42 days is 3 half-lives.