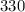Answer:
330
Explanation:
So to find x% of a, it can generally be expressed as:
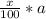 where x=percentage, and a=value. All you're doing in this equation is converting the percentage into its decimal form and then multiplying it by a to find what x% is of a. So I'm assuming 66 2/3 represents 66.6666... and not 66 * 2/3. So to make this a bit easier, we can just represent this value as one fraction, by multiplying 66 by 3 and adding that to the 2, to get:
where x=percentage, and a=value. All you're doing in this equation is converting the percentage into its decimal form and then multiplying it by a to find what x% is of a. So I'm assuming 66 2/3 represents 66.6666... and not 66 * 2/3. So to make this a bit easier, we can just represent this value as one fraction, by multiplying 66 by 3 and adding that to the 2, to get:
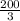
Now let's plug the values into the equation:
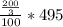
To divide the fractions, simply keep, change, flip.
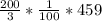
Multiply
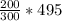
Simplify the fraction:
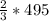
Multiply
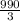
Divide: