Question

If $f(x)$ is a polynomial of degree 3, and $g(x)$ is a polynomial of degree 5, then what is the degree of polynomial $2f(x) 4g(x)$

Answer 1

degree of 8

Explanation:

Given that f(x) is a polynomial of degree 3. The cubic function (3rd degree) can be expressed as:

`\displaystyle{f(x) = ax^3 + bx^2 + cx + d}`

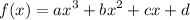
While the g(x) is a polynomial of degree 5. It can be expressed as:

`\displaystyle{g(x) = ax^5 + bx^4 + cx^3 + dx^2 + ex + f}`

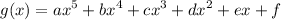
And the problem gives us to find "
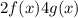`\displaystyle{2f(x)4g(x)}`". First, evaluate each terms:

2f(x)

2f(x) can be evaluated by multiplying 2 in every terms of function f(x):

`\displaystyle{2f(x) = 2(ax^3+bx^2+cx+d)}\\\\\displaystyle{2f(x) = 2ax^3+2bx^2+2cx+2d}`

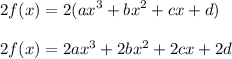
4g(x)

Similar to above one except we change to multiply from f(x) to g(x) by 4:

`\displaystyle{4g(x) = 4(ax^5 + bx^4 + cx^3 + dx^2 + ex + f)}\\\\\displaystyle{4g(x) = 4ax^5 + 4bx^4 + 4cx^3 + 4dx^2 + 4ex + 4f}`

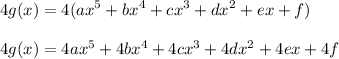
Since we are looking for the degree of polynomial, it's not necessary to bring all terms to multiply 2f(x) with 4g(x). We'll be multiplying both functions with the highest degree of individual polynomial.

The highest degree of 2f(x) is 3 which is term of
`\displaystyle{2ax^3}`

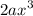
The highest degree of 4g(x) is 5 which is term of
`\displaystyle{4ax^5}`

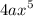
Since we are looking for the degree, we only have to evaluate the x-term with exponent:

`\displaystyle{x^3 \cdot x^5}`

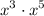
Apply the law of exponent - add both exponents together:

`\displaystyle{x^8}`

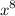
Therefore, we can conclude that the degree of polynomial is 7.

=========

In short explanation, it's not necessary to do everything. Since we are looking for degree, we only take
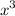`\displaystyle{x^3}` which polynomial of degree 3 and
`\displaystyle{x^5}` which is degree of 5 then multiply both terms together which result in
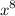`\displaystyle{x^8}` via law of exponent.

Evaluating 2f(x)4g(x) will result with same degree anyways so it's not necessary to evaluate but in case if you want to see what is 2f(x)4g(x) then I've calculated it above.