Answer:
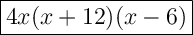
Explanation:
Given expression
4x³ + 24x² - 288x
Factorize 4x out from the expression
4x · x² + 4x · 6x - 4x · 72
4x (x² + 6x - 72)
Cross multiply to factorize the remaining polynomial expression
The meaning is to allow the factored product of the constant to add up to the first-degree term
x 12
x -6
Combine the result
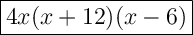
Hope this helps!! :)
Please let me know if you have any questions