Answer:
see explanation
Explanation:
using Pythagoras' identity in right triangle MOP to find OP
OP² + MP² = MO²
OP² + 7² = 25²
OP² + 49 = 625 ( subtract 49 from both sides )
OP² = 576 ( take square root of both sides )
OP =
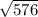 = 24
= 24
Using Pythagoras' identity in right triangle NOP
PN² + OP² = NO²
PN² + 576 = 30²
PN² + 576 = 900 ( subtract 576 from both sides )
PN² = 324 ( take square root of both sides )
PN =
 = 18 cm
= 18 cm
----------------------------------------------------------------------------
Consider a vertical line from C to AB parallel to AD
then using Pythagoras' identity in the formed right triangle
BC² = AD² + (10 - 7)²
BC² = 4² + 3² = 16 + 9 = 25 ( take square root of both sides )
BC =
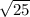 = 5
= 5
then perimeter (P) of ABCD is
P = AB + BC + CD + AD = 10 + 5 + 7 + 4 = 26 cm
The perimeter of the square is therefore 26 cm
with side s = 26 ÷ 4 = 6.5 cm
the area (A) of the square is calculated as
A = s² = 6.5² = 42.25 cm²