Answer:
The ordered pairs are(missing values in original question are underlined)
(2, 2), (3, 7), (-4,14),(4,14), (-1,-1),(1,-1)
Explanation:
The given function is
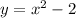
In the first two ordered pairs we are given the value of
 and all we have to do is substitute for
and all we have to do is substitute for
 in the above function and solve for
in the above function and solve for

So, for (2,...) where
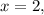
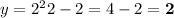
For the second pair, (3,...)
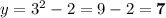
For the last two pairs, we are given what the y value is and we substitute for y in the function equation and solve for x
For (..., 14) we get
14=x^{2}-2==>16=x^{2},so x=\pm4. This means the two possible values for x are -4 and 4
For the last pair, y=-1 which gives us
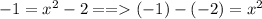
which gives the two possible values for x as
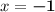 and
and
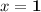
See the attached image for a visual depiction of these points