11. A club has 45 members and its membership committee has 7 members. How many different membership committees are possible?

Question

asked Aug 20, 2023 20.6k views

2 Answers

Fred Pym · Answer 1 · 2023-08-25T01:03:25+0000

Answer:
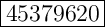
$\Large\boxed{45379620}$

Explanation:

Given information

Total members = 45

Number of membership = 7

Concept

Imagine that the membership is seating where people need to sit:

_____ _____ _____ _____ _____ _____ _____

For every position, there can be only 1 member, and 1 member can only be in one membership position, so there will not be the repetition of members.

Also, since order does not matter in assigning memberships, we use a combination

Given formula

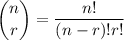
$\dbinom{n}{r}=(n!)/((n-r)!r!)$

$n=size~of~the~set\\r=number~of~selected$

Substitute values into the given formula

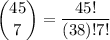
$\dbinom{45}{7}=(45!)/((38)!7!)$

Simplify the fraction by canceling out repeating values

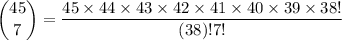
$\dbinom{45}{7}=(45*44*43*42*41*40*39*38!)/((38)!7!)$

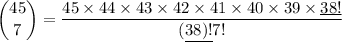
$\dbinom{45}{7}=\frac{45*44*43*42*41*40*39*\underline{38!}}{(\underline{38)!}7!}$

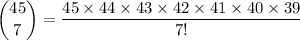
$\dbinom{45}{7}=(45*44*43*42*41*40*39)/(7!)$

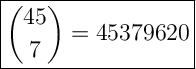
$\Large\boxed{\dbinom{45}{7}=45379620}$

Hope this helps!! :)

Please let me know if you have any questions