Question

21

a
f
h XUY
23
O
O 5 tan t
Ot cot t
Rewrite and simplify g(x) with the given subsititution* (5 Points)
5x
g (x)
2 sint (assume 0 < t < 7)
4-x²
10 sin t
2-2 sin 1
O None of these expressions
O I don't know.
O
24
Find all solutions for t (in radians) of the given equation on the interval [0,2n)* (5 Points)
8 sin 2t + sint = 0

Answer 1

Explanation:

Make the substitution first for x:

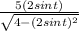`(5(2sint))/(√(4-(2sint)^2) )` and simplify a bit:

`(10sint)/(√(4-4sin^2t) )`. Factor a 4 out of the expression under the radical:

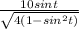`(10sint)/(√(4(1-sin^2t)) )` and pull out the perfect square in 4 as a 2:

`(10sint)/(2√(1-sin^2t) )` and divide 10 by 2 to get:

`(5sint)/(√(1-sin^2t) )`

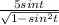
Our Pythagorean trig identity tells us that

`sin^2(t)+cos^2(t)=1` so

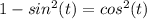`1-sin^2(t)=cos^2(t)`. Make that substitution:

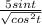`(5sint)/(√(cos^2t) )` The denominator can be simplified (the squaring of the square root each cancel out), leaving us with:

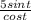`(5sint)/(cost)`. Sin over cos is the same as tangent, so our final simplification is

5tan(t)