well, we know what S(x) is, since it's given, so, after , is simply a matter of x = 2,4,6,8,10, so
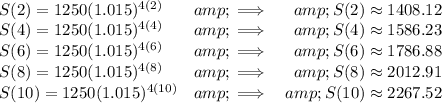
well, the tell-tale for Growth or Decay is the parenthesized term, namely the "rate of change", if it's greater than 1 is Growth, if it's less than 1 is Decay, in this case is greater than 1, is 1.015, so well, you know.
from 4 years to 10 years, how much more in interest?
well, first off let's take off the Principal of 1250 to see how much is in interest, hmmm for 4 years that'll be 336.23 and for 10 years that'll be 1017.52, so their difference is about 681.29.
what does the S-intercept mean? Check the picture below.
when the graph touches the y-axis or S-axis if you wish, the time is 0 and the amount is, well, you can see it there.