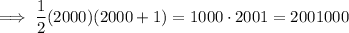Answer:
43. 20,100
44. 80,200
45. 320,400
46. 2,001,000
Explanation:
Gauss's method
General formula for the sum of the first n integers:
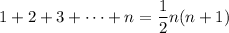
Question 43
Given sum:
Therefore, n = 200.
Substitute the value of n into the formula:
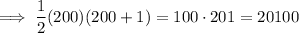
Question 44
Given sum:
Therefore, n = 400.
Substitute the value of n into the formula:
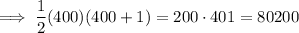
Question 45
Given sum:
Therefore, n = 800.
Substitute the value of n into the formula:
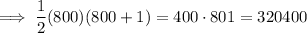
Question 46
Given sum:
Therefore, n = 2000.
Substitute the value of n into the formula: