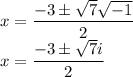Question

Complex solutions of x^2+3x+4=0?

Answer 1

`\displaystyle \large \boxed{x = ( - 3 \pm √( 7)i )/(2) }`

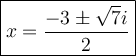
Explanation:

We are given the equation:

`\displaystyle \large{ {x}^(2) + 3x + 4 = 0}`

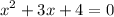
Since the expression is not factorable with real numbers, we use the Quadratic Formula.

Quadratic Formula

`\displaystyle \large{x = \frac{ - b \pm \sqrt{ {b}^(2) - 4ac} }{2a} }`

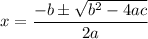
Compare the expression:

`\displaystyle \large{a {x}^(2) + bx + c = {x}^(2) + 3x + 4 }`

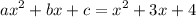
a = 1

b = 3

c = 4

Substitute a = 1, b = 3 and c = 4 in the formula.

`\displaystyle \large{x = \frac{ - 3 \pm \sqrt{ {3}^(2) - 4(1)(4)} }{2(1)} } \\ \displaystyle \large{x = ( - 3 \pm √( 9 - 16) )/(2) } \\ \displaystyle \large{x = ( - 3 \pm √( - 7) )/(2) }`

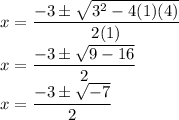
Imaginary Unit

`\displaystyle \large{i = √( - 1) }`

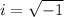
Therefore,

`\displaystyle \large{x = ( - 3 \pm √( 7) √( - 1) )/(2) } \\ \displaystyle \large{x = ( - 3 \pm √( 7)i )/(2) }`