Question

What is the solution to 3/2b + 5 < 17? Explain How.

(1) b < 8

(2) b > 8

(3) b < 18

(3) b > 18

Answer 1

Answer: [A]: " b < 8 " .
_____

Explanation:

Given:
Find the solution to: " 3/2b + 5 < 17 " ; and choose from the answer choices.

So; we have:

(3/2)b + 5 < 17 ;

Now, subtract "5" from each side of this inequality:
(3/2)b + 5 − 5 < 17 − 5 ;

To get:
(3/2)b < 12 ;

Now, let's multiply Each Side of this inequality by "2" ;

to get rid of the fraction:

" 2*(3/2)b < 12*2 " ;

{Note: "
`2 *(3)/(2)=(2)/(1)*(3)/(2)` " } ;

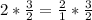Note: To simplify: "
`(2)/(1) * (3)/(2)` " ;
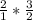Note the "2" in the denominator in the "first term" ;

And: The "2" in the denominator in the "second term" ;

Both "cancel out" to "1" ; since: "[ 2 / 2 = 2÷2 = 1 ]" ;

And: we have: "
`(1)/(1)*(3)/(1)= 1 *3 = 3` " };

_____
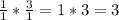and rewrite:
" 3b < 24 " ;

Now, divide Each side of the inequality by "3" ;

to isolate "b" on one side of the inequality;

and to solve for "x" ;
_____
" 3b/3 < 24/3 " ;

to get:

_____

" b < 8 " ; which corresponds to the correct answer:

Answer choice: [A]: " b < 8 " .
_____

Hope this is helpful to you! Best wishes!
_____

Answer 2

3/2b + 5 < 17

We subtract 5 from both sides of the inequality.

3/2b + 5 - 5 < 17 - 5

3/2 b < 12

Multiply both sides by 2/3.

( 2/3) * (3/2b) < (2/3) * 12

b < 8

Therefore, the correct option is alternative "A".

We would think that it is option B, but the only difference is that it changes the direction of the sign.