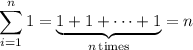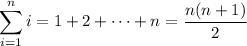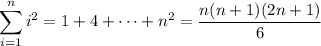Split up the interval [0, 6] into 6 equally spaced subintervals of length
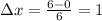 . So we have the partition
. So we have the partition
[0, 1] U [1, 2] U [2, 3] U [3, 4] U [4, 5] U [5, 6]
where the left endpoint of the
 -th interval is
-th interval is
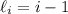
with
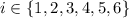 .
.
The area under
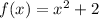 on the interval [0, 6] is then given by the definite integral and approximated by the Riemann sum,
on the interval [0, 6] is then given by the definite integral and approximated by the Riemann sum,
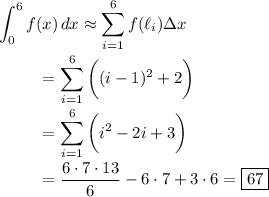
where we use the well-known sums,