Answer:
yes
Explanation:
The associative and commutative properties of multiplication allow you to rearrange the product to the form shown in the question.
Division by 2 is effectively multiplication by 1/2.
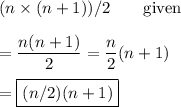
__
Additional comment
Evaluation of the expressions according to the order of operations will proceed differently for the two expressions.
For the first expression, evaluation steps are ...
- add 1 to n
- multiply the sum by n
- divide the product by 2
For the second expression, evaluation steps are ...
- divide n by 2
- add 1 to n
- multiply the results of these two operations
As we said above, the properties of multiplication ensure the results are the same either way.
As a practical matter, for integer values of n, one of n and (n+1) will be even. It is usually convenient to divide the even number by 2. This means the evaluation might be ...
- ((n+1)/2)n . . . . for odd n
- (n+1)(n/2) . . . . for even n
For certain computer representations of the numbers, results may differ depending on the specific numbers and the order of evaluation.