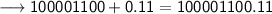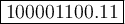Question

`{ \green \bigstar}\rm \: Convert \: ( \: 268.75 \: )_(10) \: into \: binary \: equivalent. \:`

Thank uh ~​

Answer 1

`\huge\underline{\underline{\boxed{\mathbb {SOLUTION:}}}}`

Divide 268 by 2, keeping notice of the quotient and the remainder. You will have to keep dividing the quotient by 2 until you get a quotient of zero as shown below:

`\small\longrightarrow \sf{(268)/(2) =134 \: R \: 0}`

`\small\longrightarrow \sf{(134)/(2) = \: 67 \: R \: 0}`

`\small\longrightarrow \sf{(67)/(2) = \: 33 \: R \: 1 }`

`\small\longrightarrow \sf{(33)/(2) = \: 16 \: R \: 1}`

`\small\longrightarrow \sf{(16)/(2) = \: 8 \: R \: 0}`

`\small\longrightarrow \sf{(8)/(2) = \: 4 \: R \: 0}`

`\small\longrightarrow \sf{(4)/(2) = \: 2 \: R \: 0}`

`\small\longrightarrow \sf{(2)/(2) = 1 \: R \: 0}`

`\small\longrightarrow \sf{(1)/(2) = \: 0 \: R \: 1}`

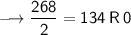
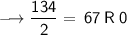
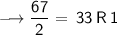
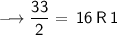
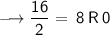
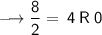
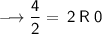
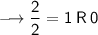
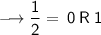
Writing out the remainder from bottom to top will give 100001100.

Multiply the decimal 0.75 by 2 and keep noting down by integer values as shown:

`\sf\longrightarrow{\small 0.75 \cdot 2 = 1.5 = 1 + 0.5}`

`\sf\longrightarrow{\small 0.5 \cdot 2 = 1.0 = 1 +0}`

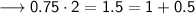
The equivalent binary for 0.75 will be 0.11.

▪
`\sf\longrightarrow{100001100 + 0.11 = 100001100.11}`



`\huge\underline{\underline{\boxed{\mathbb {ANSWER:}}}}`

`\large\boxed{\bm{100001100.11}}`