◉
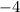

Before performing any calculation it's good to recall a few properties of integrals:
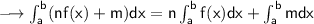
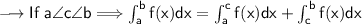
So we apply the first property in the first expression given by the question:
![\small \sf{\longrightarrow\int ^3_(-2) [2f(x) +2]dx= 2 \int ^3 _(-2) f(x) dx+ \int f^3 _(2) 2dx=18}](https://img.qammunity.org/2023/formulas/mathematics/college/khigzz9uwiqfvgm4qohk68hsh353r9u1b2.png)
And we solve the second integral:
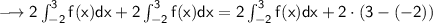
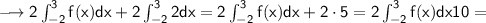
Then we take the last equation and we subtract 10 from both sides:
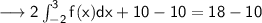
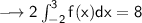
And we divide both sides by 2:
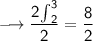
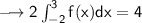
Then we apply the second property to this integral:
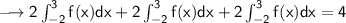
Then we use the other equality in the question and we get:
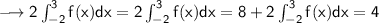
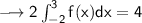
We substract 8 from both sides:
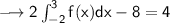
•