Answer:
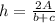
Explanation:
Original Equation:
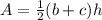
Divide both sides by height
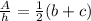
Raise both sides to the exponent -1 :

Rewrite using the definition of a negative exponent:
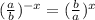
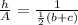
Multiply 1/2 by (b+c)
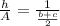
Keep, change, flip
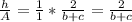
Multiply both sides by A
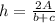
Also I forgot to mention but the exponent (-1) can be ignored after you flip it, since:
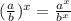 , but since in our case the exponent is 1, and
, but since in our case the exponent is 1, and
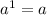 , so there's really no need to write out the distribution part, since we just get the same fraction, after flipping it.
, so there's really no need to write out the distribution part, since we just get the same fraction, after flipping it.