![\displaystyle \lim_(n\to \infty) ~~ \cfrac{5n^2}{7n^3-4}\qquad \implies \lim_(n\to \infty) ~~ \stackrel{\textit{using L'Hopital's rule}}{\cfrac{(d)/(dn)[5n^2]}{(d)/(dn)[7n^3-4]}}\implies \lim_(n\to \infty) ~~\cfrac{10n}{21n^2}\implies 0](https://img.qammunity.org/2023/formulas/mathematics/college/h98di3leg6p8o3vbzu79inhnao6lcledxf.png)
now, how do we get 0?
well, simple, hmmmm let me put a few values in
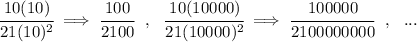
in math lingo, on every iteration or change of the variable "n", the numerator is increasing but at a lower rate than the denominator, the denominator is increasing much more on every iteration, namely the denominator is moving faster and thus as "n" increases ever to infinity, the fraction becomes smaller and smaller and smaller, ever getting closer to 0.