Answer:
y = 2x² − 12x + 8
Explanation:
FIRST METHOD :
y = 2x² − 12x + 8
= (2x² − 12x) + 8
= 2 (x² − 6x) + 8
= 2 (x² − 6x + 9 − 9 ) + 8
= 2 (x² − 6x + 9) − 2×9 + 8
= 2 (x² − 6x + 9) − 18 + 8
= 2 (x² − 6x + 9) − 10
= 2 (x − 3)² − 10
Then ,the equation has a extremum value of (3,-10)
Since the number 2 in the equation y = = 2 (x − 3)² − 10 is greater than 0
(2 > 0) , the graph (parabola) opens upward
Therefore ,the extremum (3,-10) is a minimum.
SECOND METHOD :
the graph of a function of the form f(x) = ax² + bx + c
has an extremum at the point :

in the equation : f(x) = 2x² − 12x + 8
a = 2 ; b = -12 ; c = 8
Then
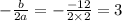
Then

the graph of a function f(x) = 2x² − 12x + 8
has an extremum at the point (3 , -10)
Since the parabola opens up ,then the extremum (3,-10) is a minimum.