Question

Given 3x^2+x-4/x-1 what are the domain and range

Answer 1

• doman: x ≠ 1
• range: y ≠ 7

Explanation:

The domain is the horizontal extent of the graph, the set of x-values for which the function is defined. The range is the vertical extent of the graph, the set of y-values defined by the function.

Simplified

The given function is undefined where its denominator is zero, at x=1. Everywhere else, it can be simplified to ...

`(3x^2+x-4)/(x-1)=((x-1)(3x+4))/((x-1))=3x+4\quad x\\e 1`

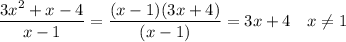
Domain

The simplified function (3x+4) is defined for all values of x except x=1. The simplest description is ...

x ≠ 1

In interval notation, this is ...

(-∞, 1) ∪ (1, ∞)

Range

The simplified function is capable of producing all values of y except the one corresponding to x=1: 3(1)+4 = 7. The simplest description is ...

y ≠ 7

In interval notation, this is ...

(-∞, 7) ∪ (7, ∞)