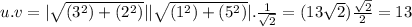We need to use a technique called dot multiplication. In this technique, we multiply the magnitude of two given vectors by the value of the angle between them.
In the question, the value of the angle between two vectors
 and the coordinates of the two vectors are given. Let's multiply them by the dot product to get the result.
and the coordinates of the two vectors are given. Let's multiply them by the dot product to get the result.
Formula:
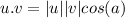

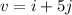
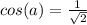
To find the magnitude of a vector, we square the coordinates, add them up and take the square root of the result.
Result: