Answer:
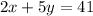
Explanation:
Median of a triangle: A line segment that connects a vertex of a triangle to the midpoint of the opposite side.
Vertex: The point where any two sides of a triangle meet.
Given vertices of a triangle:
- A = (-2, 9)
- B = (-33, 13)
- C = (-21, 25)
Step 1
Find the midpoint of BC (Point D) by using the Midpoint formula.
Midpoint between two points
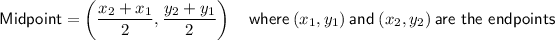
Define the endpoints:
Substitute the defined endpoints into the formula:
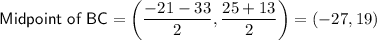
Therefore, D = (-27, 19).
Step 2
Find the slope of the median (line AD) using the Slope formula.
Define the points:
Substitute the defined points into the Slope formula:
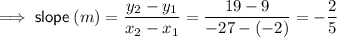
Therefore, the slope of the median is -²/₅.
Step 3
Substitute the found slope and one of the points into the Point-slope formula to create an equation for the median.
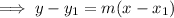
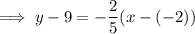
Simplify and rearrange the equation so it is in standard form Ax+By=C:
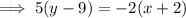
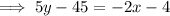
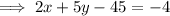
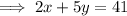
Conclusion
Therefore, the equation of the median is:
2x + 5y = 41