Answer:
Approximately
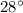 .
.
Step-by-step explanation:
The refractive index of the air
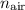 is approximately
is approximately
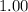 .
.
Let
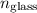 denote the refractive index of the glass block, and let
denote the refractive index of the glass block, and let
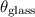 denote the angle of refraction in the glass. Let
denote the angle of refraction in the glass. Let
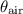 denote the angle at which the light enters the glass block from the air.
denote the angle at which the light enters the glass block from the air.
By Snell's Law:
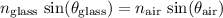 .
.
Rearrange the Snell's Law equation to obtain:
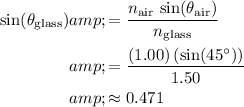 .
.
Hence:
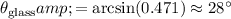 .
.
In other words, the angle of refraction in the glass would be approximately
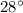 .
.