Question

Solve the following initial value problem.

d²s
dt²
= -36cos(6t+n), s'(0) = 100, s(0) = 0
S=
(Type an exact answer, using * as needed.)

Answer 1

For starters,

`\cos(6t+\pi) = \cos(6t) \cos(\pi) - \sin(6t) \sin(\pi) = -\cos(6t)`

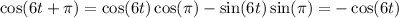
Now by the fundamental theorem of calculus, integrating both sides gives

`\displaystyle (ds)/(dt) = s'(0) + \int_0^t 36 \cos(6u) \, du = 100 + 6 \sin(6t)`

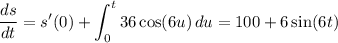
Integrating again, we get

`\displaystyle s(t) = s(0) + \int_0^t (100 + 6\sin(6u)) \, du = \boxed{100t - \cos(6t) + 1}`

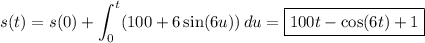
Alternatively, you can work with antiderivatives, then find the particular constants of integration later using the initial values.

`\displaystyle \int (d^2s)/(dt^2) \, dt = \int 36\cos(6t) \, dt \implies (ds)/(dt) = 6\sin(6t) + C_1`

`\displaystyle \int (ds)/(dt) \, dt = \int (6\sin(6t) + C_1) \, dt \implies s(t) = -\cos(6t) + C_1t + C_2`

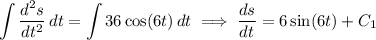
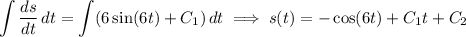
Now,

`s(0) = 0 \implies 0 = -1 + C_2 \implies C_2 = 1`

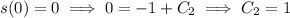
and

`s'(0) = 100 \implies 100 = 0 + C_1 \implies C_1 = 100`

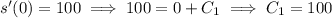
Then the particular solution to the IVP is

`s(t) = -\cos(6t) + 100t + 1`

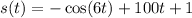
just as before.