Answer: 65
============================================================
Step-by-step explanation:
We'll need to compute the difference quotient. In this case, we need to find what
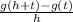 is equal to. It's called a difference quotient because there's a subtraction in the numerator (aka "difference") and we're dividing to form the quotient.
is equal to. It's called a difference quotient because there's a subtraction in the numerator (aka "difference") and we're dividing to form the quotient.
The idea is that as h approaches 0, then that expression I wrote will approach the derivative we're after. Keep in mind that h will technically never get to 0 itself. It only gets closer and closer.
Anyways, let's compute
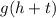 first
first

Then we'll subtract off g(t)
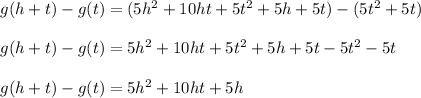
A very important thing to notice: the terms that don't have any 'h's in them have been canceled out (eg: 5t^2 combined with -5t^2 added to 0). Why is this important? It's because we need to factor 'h' out and we'll have a pair of 'h's cancel like so
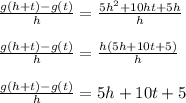
The left hand side cannot have h = 0, or else we have a division by zero error. But if we approached 0 (not actually getting there), then the expression 5h+10t+5 will approach 5(0)+10t+5 = 10t+5
---------------------
In short: The derivative of
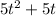 is
is
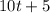
In terms of symbols,
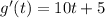
Later on in calculus, you'll learn a shortcut so you won't have to compute the difference quotient every time you need a derivative. Refer to the power rule for more information.
After we find the derivative, it's as straight forward as plugging in t = 6 to compute g ' (6)
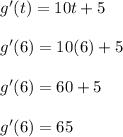
Side note: This tells us that the slope of the tangent line is m = 65 when t = 6. In other words, this line is tangent to g(t) when t = 6, and this particular tangent line has slope m = 65.