Question

What is the center of the ellipse x2+5y2–45=0?

Write your answer in simplified, rationalized form.
(___,___)

Answer 1

Center is at (0,0)

Explanation:

An equation of ellipse in standard form is:

`\displaystyle{((x-h)^2)/(a^2)+((y-k)^2)/(b^2) = 1`

Where center is at point (h,k)

From the equation of
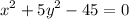`\displaystyle{x^2+5y^2-45=0}`. First, we add 45 both sides:

`\displaystyle{x^2+5y^2-45+45=0+45}\\\\\displaystyle{x^2+5y^2=45}`

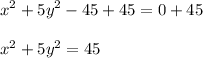
Convert into the standard form with RHS (Right-Hand Side) equal to 1 by dividing both sides by 45:

`\displaystyle{(x^2)/(45)+(5y^2)/(45)=(45)/(45)}\\\\\displaystyle{(x^2)/(45)+(y^2)/(9)=1}`

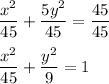
Therefore, the center of ellipse is at (0,0) since there are no values of h and k.