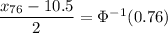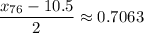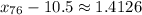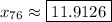a. This information is given to you.
b. We want to find
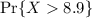
so we first transform
 to the standard normal random variable
to the standard normal random variable
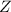 with mean 0 and s.d. 1 using
with mean 0 and s.d. 1 using
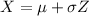
where
 are the mean/s.d. of
are the mean/s.d. of
 . Now,
. Now,
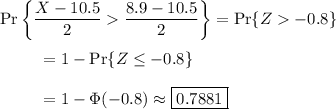
where
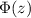 is the CDF for
is the CDF for
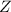 .
.
c. The 76th percentile is the value of
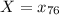 such that
such that
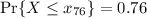
Transform
 to
to
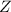 and apply the inverse CDF of
and apply the inverse CDF of
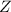 .
.