Question

F(x)

Which type of function describes f(x)?
•
Rational
Polynomial
O Logarithmic
• Exponential

Answer 1

Answer: exponential

Explanation:

Answer 2

Exponential function

`y=1.25(2)^x`

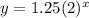
Explanation:

Definitions

Asymptote: a line that the curve gets infinitely close to, but never touches.

Hole: a point on the graph where the function is not defined.

Polynomial Function

`f(x)=a_nx^n+a_(n-1)x^(n-1)+...+a_2x^2+a_1x+a_0`

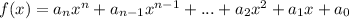
An equation containing variables with non-negative integer powers and coefficients, that involves only the operations of addition, subtraction and multiplication.

A continuous function with no holes or asymptotes.

Rational Function

`f(x)=(h(x))/(g(x))`

An equation containing at least one fraction whose numerator and denominator are polynomials.

A rational function has holes and/or asymptotes.

• A rational function has holes where any input value causes both the numerator and denominator of the function to be equal to zero.

• A rational function has vertical asymptotes where the denominator approaches zero.

• If the degree of the numerator is smaller than the degree of the denominator, there will be a horizontal asymptote at y = 0.

• If the degree of the numerator is the same as the degree of the denominator, there will be a horizontal asymptote at y = ratio of leading coefficients.

• If the degree of the numerator is exactly one more than the degree of the denominator, slant asymptotes will occur.

Logarithmic Function

`f(x) =\log_ax`

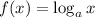
A continuous function with a vertical asymptote.

A logarithmic function has a gradual growth or decay.

Exponential Function

`f(x)=ab^x`

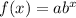
The variable is the exponent.

A continuous function with a horizontal asymptote.

An exponential function has a fast growth or decay.