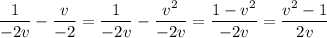Multiply both sides by
 .
.

Substitute
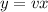 , so
, so
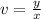 and
and
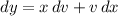 .
.
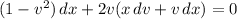
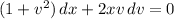
Separate the variables.
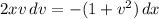
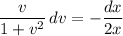
Integrate both sides
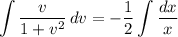
On the left side, substitute
 and
and
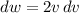 .
.

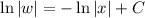
Solve for
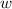 , then
, then
 , then
, then
 .
.

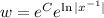
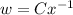
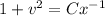
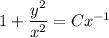

Your mistake is in the first image, between third and second lines from the bottom. (It may not be the only one, it's the first one that matters.)
You incorrectly combine the fractions on the left side.