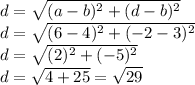Question

Csn u please help me o have no idea

Answer 1

D.= √29

Explanation:

Greetings!

The distance between the two complex numbers,

Z₁=a+bi and Z₂=c+di in the complex plane is

`d = \sqrt{(c - a) {}^(2) + (d - b) {}^(2) }`

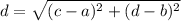
In the Cartesian plane, the distance between, one point and other is (x₁,y₁) and (x₂,y₂) is the distance formula is

`d = √((X₂-X₁)² + (Y₂-Y₁)²)`

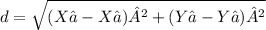
To find the distance between the two complex numbers using the formula

`d = \sqrt{(c - a) {}^(2) + (d - b) {}^(2) }`

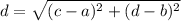
where,

• a=4
• b=3
• c=6
• d=-2

`d = \sqrt{(a - b) {}^(2) + (d - b) {}^(2) } \\ d = \sqrt{(6 - 4) {}^(2) + ( - 2 - 3) {}^(2) } \\ d = \sqrt{(2) {}^(2) + ( - 5) {}^(2) } \\ d = √(4 + 25) = √(29 \\ )`