Answer:
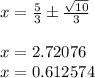
Explanation:
The quadratic equation is:
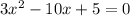
The roots (solutions) of a quadratic equation of the form
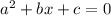
are
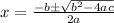
in this case we have a = 3, b = -10, and c = 5
So, substituting for a, b and c we get
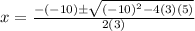
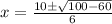
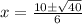
Simplifying we get
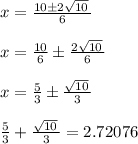 (First root/solution)
(First root/solution)
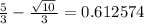 (Second root/solution)
(Second root/solution)