Question

A polygon ABCD is inscribed in a circle. Find m angle D A B.

Answer 1

Answer:
`\Large\boxed{\angle DAB=62^\circ}`

Concept:

Here, we need to know about the idea of a cyclic quadrilateral.

In a cyclic quadrilateral, the sum of either pair of opposite angles is supplementary, which means they add up to 180°.

Please refer to the attachment below for a graphical explanation

Solve:

Given information

∠DAB = 2x + 4

∠ABC = 4y + 4

∠BCD = 4x + 2

∠CDA = 3y + 8

Derived formula from the concept

∠DAB + ∠BCD = 180°

∠ABC + ∠CDA = 180° (Not Important)

Substitute values into the formula that includes ∠DAB

∠DAB + ∠BCD = 180°

(2x + 4) + (4x + 2) = 180

Combine like terms

2x + 4 + 4x + 2 = 180

2x + 4x + 4 + 2 = 180

6x + 6 = 180

Subtract 6 on both sides

6x + 6 - 6 = 180 - 6

6x = 174

Divide 6 on both sides

6x / 6 = 174 / 6

x = 29

Substitute values into the angle expression of ∠DAB

∠DAB = 2x + 4

∠DAB = 2 (29) + 4

∠DAB = 58 + 4

`\Large\boxed{\angle DAB=62^\circ}`

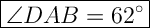
Hope this helps!! :)

Please let me know if you have any questions