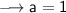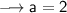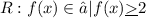Question

What is the range of the function f(x) = |x + 4| + 2?

R: f(x) ∈ ℝ
R: f(x) ≥ 2
R: f(x) ∈ ℝ
R: f(x) ∈ ℝ

Answer 1

`\huge\underline{\underline{\boxed{\mathbb {SOLUTION:}}}}`

Given:

▪
`\longrightarrow \sfx + 4`

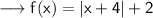
You need to remember that the form of an Absolute Value Function is:

• For the vertex:

`\small\longrightarrow \sf{H= \: \: x -coordinate}`

`\small\longrightarrow \sf{K= y-coordinate}`

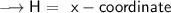
• For the definition:

If "a" is positive (+) , then the range of the function is:

`\small\longrightarrow \sf{R:y \: \underline > \: k}`

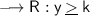
If "a" is negative (-), the range of the function is:

`\small\longrightarrow \sf{R: y \: \underline < \: k}`

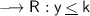
In this case we can identify that:

`\small\longrightarrow \sf{a = 1}`

`\small\longrightarrow\sf{a = 2}`

`\huge\underline{\underline{\boxed{\mathbb {ANSWER:}}}}`

`\large \bm{R: f(x) \underline > 2}`