Answer:
1240 mmHg
Step-by-step explanation:
Since volume is being held constant, we can use the following variation of the Ideal Gas Law to find the new pressure.
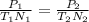
In the equation, "P₁", "T₁", and "N₁" represent the initial pressure, temperature, and moles. "P₂", "T₂", and "N₂" represent the final pressure, temperature, and moles. Your answer should have 3 sig figs to match the sig figs of the given values.
P₁ = 825 mmHg P₂ = ? mmHg
T₁ = 303 K T₂ = 273 K
N₁ = 1.50 moles N₂ = 1.50 + 1.00 = 2.50 moles
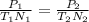 <----- Formula
<----- Formula
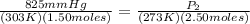 <----- Insert values
<----- Insert values
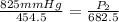 <----- Simplify denominators
<----- Simplify denominators
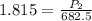 <----- Simplify left side
<----- Simplify left side
 <----- Multiply both sides by 682.5
<----- Multiply both sides by 682.5
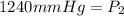 <----- Apply sig figs
<----- Apply sig figs