Answer:
(0, -3)
Explanation:
This system of equations consists of two equations. There are 3 main ways to solve a system of equations:
- Graphing (The solution is the point where the two lines intersect)
- Substitution
- Elimination
First, start by having the variables on one side.
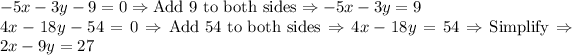
Solve Using Elimination
This method is the easiest to use in this situation.
In this method, we increase equations by a certain factor in order to eliminate one variable.
We can see that 3y in the first equation can be multiplied by 6 in order to obtain the 18y in the second equation. Therefore, we can multiply the whole first equation by 6:
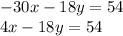
Now, subtract the two equations to eliminate y.
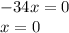
Plug in 0 to x in either of the equations to solve for y:
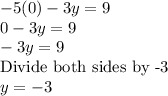
OR
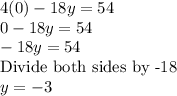
Therefore:
(x, y) = (0, -3)