Hi :)
————————————————
We'll use sohcahtoa to solve this problem

Looking at our triangle, we can clearly see that we have :
- adj. side = 48 (adjacent to the angle)
- hyp. k (the one we need)
Set up the ratio
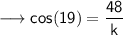
solve for k
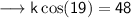 > multiply both sides by k to clear the fraction
> multiply both sides by k to clear the fraction
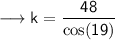 > divide both sides by cos (19)
> divide both sides by cos (19)
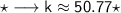
:)