The span of 3 vectors can have dimension at most 3, so 9 is certainly not correct.
Check whether the 3 vectors are linearly independent. If they are not, then there is some choice of scalars
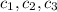 (not all zero) such that
(not all zero) such that
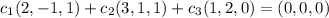
which leads to the system of linear equations,
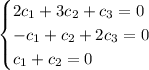
From the third equation, we have
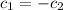 , and substituting this into the second equation gives
, and substituting this into the second equation gives

and in turn,
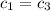 . Substituting these into the first equation gives
. Substituting these into the first equation gives

which tells us that any value of
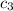 will work. If
will work. If
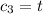 , then
, then
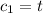 and
and
 . Therefore the 3 vectors are not linearly independent, so their span cannot have dimension 3.
. Therefore the 3 vectors are not linearly independent, so their span cannot have dimension 3.
Repeating the calculations above while taking only 2 of the given vectors at a time, we see that they are pairwise linearly independent, so the span of each pair has dimension 2. This means the span of all 3 vectors taken at once must be 2.